Roulette Logarithms
- Roulette Logarithms In Python
- Roulette Logarithm
- Roulette Logarithms In Exponential
- Karl Roulette Logarithm
- Roulette Logarithm Strategy
By Ion Saliu,
Founder of Gambling Mathematics, Founder of Probability Theory of Life
I. Theory of Probability Leading to Fundamental Formula of Gambling (FFG)
II. Fundamental Table of Gambling (FTG)
III. Fundamental Formula of Gambling: Games Other Than Coin Tossing
IV. Ion Saliu's Paradox or Problem of N Trials in Gambling Theory
V. Practical Dimension of Fundamental Formula of Gambling
VI. Resources in Theory of Probability, Mathematics, Statistics, Software
- The 'Roulette Mining' program is a universal powerful calculator of bets that will double (!) deposit in any casino. This program works with any kind of roulette, in any casino. The auto-clicker feature is only available for PC users.
- Roulette Logarithm Wins June 2, 2019 Is important to play Roulette in a casino that has quick withdrawals cause if your Pending Withdrawals are there even after 3 days than you are tempting to cancel. So in this website you will find only the website which has quick Withdrawals even in a few minutes!
Roulettephysics.com ← How to win at roulette Roulette-computers.com ← Hidden electronics that beat roulette Roulettetraining.com ← Free roulette downloads Roulettestrategyreviews.com ← Add & read reviews Free Roulette Simulator ← Simulated real wheel physics LandSharing.org: Improving Living Standards. 68426 Posts 2542 Topics. How to win at roulette using science: Expert reveals the physics behind predicting where the ball will land. In the late 1970s a group tried to beat a roulette wheel with computers.
The final version published in December 1997; first capture by the WayBack MachineThe casinos know roulette is being beaten, and they know professional roulette strategy players are a real threat. But they rely on detecting professional players before they win too much. Below is a collection of news articles. Some of the information is inaccurate, and it explains barely a fraction of the principles that make roulette.
(web.archive.org) April 17, 2000.- Presenting the most astonishing formula in gambling mathematics, probability theory at large, widely known now as FFG. Indeed, it is the most essential formula of theory of probability. This formula was directly derived from the most fundamental formula of probability: Number of favorable cases, n, over Total possible cases, N: n / N. Abraham de Moivre, a French/English-refugee mathematician and philosopher discovered the first steps of this formula that explains the Universe the best. I believe Monsieur de Moivre was frightened by the implications of finalizing such formula would have led to: The absurdity of the concept of God. I did finalize the formula, for the risks in my lifetime pale by comparison to the eighteenth century. God, no doubt, represents the limit of mathematical absurdity, therefore of all Absurdity.
And thusly we discovered here the much-feared mathematical concept of Degree of Certainty, DC. I introduced the DC concept in the year of grace 1997, or 1997+1 years after tribunicia potestas were granted to Octavianus Augustus (the point in time humans started the year count of Common Era, still in use). The Internet search on Degree of Certainty, DC yielded one and only one result in 1998: This very Web page (zero results in 1997, for DC was introduced in December of that glorious year, with some beautiful snowy days… just before the Global Warming debate started…) For we shall always be mindful that nothing comes in absolute certainty; everything comes in degrees of certainty — Never zero, Never absolutely. “Never say never; never say forever!”
- The degree of certainty DC rises exponentially with the increase in the number of trials N while the probability p is always the same or constant.
- DC = 1 – (1 – p) ^ N
- Simultaneously, the opposite event, the losing chance, decreases exponentially with an increase in the number of trials. That's the fundamental reason why the infamous gambler's fallacy is an obvious absurdity.
1. Theory of Probability Leading to the Fundamental Formula of Gambling
It has become common sense the belief that persistence leads to success. It might be true for some life situations, sometimes. It is never true, however, for gambling and games of chance in general. Actually, in gambling persistence leads to inevitable bankruptcy. I can prove this universal truth mathematically. I will not describe the entire scientific process, since it is rather complicated for all readers but a few. The algorithm consists of four phases: win N consecutive draws (trials); lose N consecutive trials;Roulette Logarithms In Python
not to lose N consecutive draws; win within N consecutive trials.• I will simplify the discourse to its essentials. You may want to know the detailed procedure leading to this numerical relation. Read: Mathematics of the Fundamental Formula of Gambling (FFG).
•• Visit the software download site (in the footer of this page) to download SuperFormula; the extraordinary software automatically does all FFG calculations, plus several important statistics and probability functions.
The probability and statistical program allows you to calculate the number of trials N for any degree of certainty DC. Plus, you can also calculate the very important binomial distribution formula (BDF) and binomial standard deviation (BSD), plus dozens of statistics and probability functions.
Let's suppose I play the 3-digit lottery game (pick 3). The game has a total of 1,000 combinations. Thus, any particular pick-3 combination has a probability of 1 in 1,000 (we write it 1/1,000). I also mention that all combinations have an equal probability of appearance. Also important - and contrary to common belief — the past draws do count in any game of chance. Pascal demonstrated that truth hundreds of years ago.
Evidently, the same-lotto-game combinations have an equal probability, p — always the same — but they appear with different statistical frequencies. Standard deviation plays an essential role in random events. The Everything, that is; for everything is random. Most people don't comprehend the concept of all-encompassing randomness because phenomena vary in the particular probability, p, and specific degree of certainty, DC, directly influenced by the number of trials, N. Please read an important article here: Combination 1 2 3 4 5 6: Probability and Reality. A 6-number lotto combination such as 1 2 3 4 5 6 should have appeared by now at least once, considering all the drawings in all lotto-6 games ever played in the world. It hasn't come out and will not appear in my lifetime... I bet on it... even if I live 100 years after 2060, when Isaac Newton calculated that the world would end based on his mathematical interpretation of the Bible! (Newton and Einstein belong to the special class of the most intelligent mystics in human and natural history.) Instead, other lotto combinations, with a more natural standard devi(l)ation (yes, deviation), will repeat in the same frame of time.
As soon as I choose a combination to play (for example 2-1-4) I can't avoid asking myself: 'Self, how many drawings do I have to play so that there is a 99.9% degree of certainty my combination of 1/1,000 probability will come out?'
My question dealt with three elements:
• degree of certainty that an event will appear, symbolized by DC
• probability of the event, symbolized by p
• number of trials (events), symbolized by N
I was able to answer such a question and quantify it in a mathematical expression (logarithmic) I named the Fundamental Formula of Gambling (FFG):
The Fundamental Formula of Gambling is an historic discovery in theory of probability, theory of games, and gambling mathematics. The formula offers an incredibly real and practical correlation with gambling phenomena. As a matter of fact, FFG is applicable to any sort of highly randomized events: lottery, roulette, blackjack, horse racing, sports betting, even stock trading. By contrast, what they call theory of games is a form of vague mathematics: The formulae are barely vaguely correlated with real life.
2. The Fundamental Table of Gambling (FTG)
Substituting DC and p with various values, the formula leads to the following, very meaningful and useful table. You may want to keep it handy and consult it especially when you want to bet big (as in a casino).Let's try to make sense of those numbers. The easiest to understand are the numbers in the column under the heading p=1/2. It analyzes the coin tossing game of chance. There are 2 events in the game: heads and tails. Thus, the individual probability for either event is p = 1/2. Look at the row 50%: it has the number 1 in it. It means that it takes 1 event (coin toss, that is) in order to have a 50-50 chance (or degree of certainty of 50%) that either heads or tails will come out. More explicitly, suppose I bet on heads. My chance is 50% that heads will appear in the 1st coin toss. The chance or degree of certainty increases to 99.9% that heads will come out within 10 tosses!
Even this easiest of the games of chance can lead to sizable losses. Suppose I bet $2 before the first toss. There is a 50% chance that I will lose. Next, I bet $4 in order to recuperate my previous loss and gain $2. Next, I bet $8 to recuperate my previous loss and gain $2. I might have to go all the way to the 9th toss to have a 99.9% chance that, finally, heads came out! Since I bet $2 and doubling up to the 9th toss, two to the power of 9 is 512. Therefore, I needed $512 to make sure that I am very, very close to certainty (99.9%) that heads will show up and I win . . . $2!
Very encouraging, isn't it? Actually, it could be even worse: It might take 10 or 11 tosses until heads appear! This dangerous form of betting is called a Martingale system. You must know how to do it — study this book thoroughly and grasp the new essential concepts: Number of trials N and especially the Degree of Certainty DC (in addition to the probability p).
Most people still confuse probability for degree of certainty...or vice versa. Probability in itself is an abstract, lifeless concept. Probability comes to life as soon as we conduct at least one trial. The probability and degree of certainty are equal for one and only one trial (just the first one...ever!) After that quasi-impossible event (for coin tossing has never been stopped after one flip by any authority), the degree of certainty, DC, rises with the increase in the number of trials, N, while the probability, p, always stays constant. No one can add faces to the coin or subtract faces from the die, for sure and undeniably. But each and every one of us can increase the chance of getting heads (or tails) by tossing the coin again and again (repeat of the trial).
Normally, though, you will see that heads (or tails) will appear at least once every 3 or 4 tosses (the DC is 90% to 95%). Nevertheless, this game is too easy for any player with a few thousand dollars to spare. Accordingly, no casino in the world would implement such a game. Any casino would be a guaranteed loser in a matter of months! They need what is known as house edge or percentage advantage. This factor translates to longer losing streaks for the player, in addition to more wins for the house! Also, the casinos set limits on maximum bets: the players are not allowed to double up indefinitely.
A few more words on the house advantage (HA). The worst type of gambling for the player is conducted by state lotteries. In the digit lotteries, the state commissions enjoy typically an extraordinary 50% house edge!!! That's almost 10 times worse than the American roulette -- considered by many a suckers' game! (But they don't know there is more to the picture than meets the eye!)
In order to be as fair as the roulette, the state lotteries would have to pay $950 for a $1 bet in the 3-digit game. In reality, they now pay only $500 for a $1 winning bet!!! Remember, the odds are 1,000 to 1 in the 3-digit game...
If private organizations, such as the casinos, would conduct such forms of gambling, they would surely be outlawed on the grounds of extortion! In any event, the state lotteries defy all anti-trust laws: they do not allow the slightest form of competition! Nevertheless, the state lotteries may conduct their business because their hefty profits serve worthy social purposes (helping the seniors, the schools, etc.) Therefore, lotteries are a form of taxation - the governments must tell the truth to their constituents...
3. Fundamental Formula of Gambling: Games Other Than Coin Tossing
Dice rolling is a more difficult game and it is illustrated in the column p=1/6. I bet, for example, on the 3-point face. There is a 50% chance (DC) that the 3-point face will show up within the first 3 rolls. It will take, however, 37 rolls to have a 99.9% certainty that the 3-point face will show up at least once. If I bet the same way as in the previous case, my betting capital should be equal to 2 to the power of 37! It's already astronomical and we are still in easy-gambling territory!
Let's go all the way to the last column: p=1/1,000. The column illustrates the well-known3-digitlottery game. It is extremely popular and supposedly easy to win. Unfortunately, most players know little, if anything, about its mathematics. Let's say I pick the number 2-1-4 and play it every drawing. I only have a 10% chance (DC) that my pick will come out winner within the next 105 drawings!
The degree of certainty DC is 50% that my number will hit within 692 drawings! Which also means that my pick will not come out before I play it for 692 drawings. So, I would spend $692 and maybe I win $500! If the state lotteries want to treat their customers (players like you and me) more fairly, they should pay $690 or $700 for a $1 winning ticket. That's where the 50-50 chance line falls.
In numerous other cases it's even worse. I could play my daily-3 number for 4,602 drawings and, finally, win. Yes, it is almost certain that my number will come out within 4,602 or within 6,904 drawings! Real life case: Pennsylvania State Lottery has conducted over 6,400 drawings in the pick3 game. The number 2,1,4 has not come out yet!...
All lottery cases and data do confirm the theory of probability and the formula of bankruptcy... I mean of gambling! By the way, it is almost certain (99.5% to 99.9%) that the number 2-1-4 will come out within the next 400-500 drawings in Pennsylvania lottery. But nothing is 100% certain, not even... 99.99%!
We don't need to analyze the lotto games. The results are, indeed, catastrophic. If you are curious, simply multiply the numbers in the last column by 10,000 to get a general idea. To have a 99.9% degree of certainty that your lotto (pick-6) ticket (with 6 numbers) will come out a winner, you would have to play it for over 69 million consecutive drawings! At a pace of 100 drawings a year, it would take over 690,000 years!
4. Ion Saliu's Paradox or Problem of N Trials
We can express the probability as p = 1/N; e.g. the probability of getting one point face when rolling a die is 1 in 6 or p = 1/6; the probability of getting one roulette number is 1 in 38 or p = 1/38. It is common sense that if we repeat the event N times we expect one success. That might be true for an extraordinarily large number of trials. If we repeat the event N times, we are NOT guaranteed to win. If we play roulette 38 consecutive spins, the chance to win is significantly less than 1!A step in the Fundamental Formula of Gambling leads to this relation:
 0.632120558828558...
0.632120558828558...I tested for N = 100,000,000 … N = 500,000,000 … N = 1,000,000,000 (one billion) trials. The results ever so slightly decrease, approaching the limit … but never surpass the limit!
When N = 100,000,000, then DC = .632120560667764...
When N = 1,000,000,000, then DC = .63212055901829...
(Calculations performed by SuperFormula, option C = Degree of Certainty (DC), then option 1 = Degree of Certainty (DC), then option 2 = The program calculates p.)
If the probability is 1/N and we repeat the event N times, the degree of certainty is 1 — (1/e), when N tends to infinity. I named this relation: Ion Saliu Paradox of N Trials. Read more on my Web pages: Theory of Probability: Best introduction, formulae, algorithms, software and Mathematics of Fundamental Formula of Gambling.
5. Practical Dimension of Fundamental Formula of Gambling
There is more info on this topic on the next page. It reveals the dark side of the Moon, so to speak. The governments hide the truth when it comes to telling it all; and the Internet is incredibly prone to fraudulent gambling. Read revealing facts: Lottery, Lotto, Gambling, Odds, House Edge, Fraud.
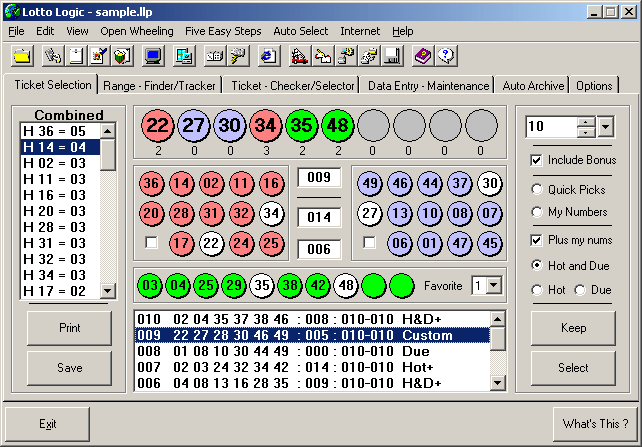
| • The Fundamental Formula of Gambling does not explicitly or implicitly serve as a gambling system. It represents pure mathematics. Users who apply the numerical relations herein to their own gambling systems do so at their risk entirely. I, the author, do apply the formula to my gambling and lottery systems. I will show you how to use the gambling formula, my application MDIEditor and Lotto and the lotto systems that come with the application. I will put everything in a winning lotto strategy that targets the third prize in lotto games (4 out of 6). •• At later times, I also released gambling systems, strategies for: Roulette, blackjack, baccarat, horse racing, sports betting. Is it all? Probably you'll find some more around here… Click here to go to the lottery strategy, systems, software page |
Read Ion Saliu's first book in print: Probability Theory, Live!
~ Discover profound philosophical implications of the Fundamental Formula of Gambling (FFG), including mathematics, probability, formula, gambling, lottery, software, degree of certainty, randomness.
6. Resources in Theory of Probability, Mathematics, Statistics, Combinatorics, Software
See a comprehensive directory of the pages and materials on the subject of theory of probability, mathematics, statistics, combinatorics, plus software.- Theory of Probability: Best introduction, formulae, algorithms, software.
- Bayes Theorem, Conditional Probabilities, Simulation; Relation to Ion Saliu's Paradox.
- Standard Deviation: Theory, Algorithm, Software.
Standard deviation: Basics, mathematics, statistics, formula, software, algorithm. - Standard Deviation, Gauss, Normal, Binomial, Distribution
Calculate: Median, degree of certainty, standard deviation, binomial, hypergeometric, average, sums, probabilities, odds. - Combinatorial Mathematics: Calculate, Generate Exponents, Permutations, Sets, Arrangements, Combinations for Any Numbers and Words.
- Caveats in Theory of Probability.
- The Best Strategy for Lottery, Gambling, Sports Betting, Horse Racing, Blackjack, Roulette.
- Birthday ParadoxProbability Formula, Odds of Duplication, Software.
- Monty Hall Paradox, 3-Door Problem, Probability Paradoxes.
- Couple Swapping, Husband Wife Swapping, Probability, Odds.
- Download Probability, Mathematics, StatisticsSoftware.
Home Search New Writings Odds, Generator Contents Forums Sitemap
You may think roulette computers are always sophisticated pieces of hardware. In actual fact, most are very simplistic, although people that sell them want to you believe it is space-age technology. Here I will explain the simplest possible roulette computer algorithm, and it is used by almost every roulette computer.
Understanding What Makes Roulette Beatable
First we'll need to identify various parts of the wheel so you know what I'm talking about:
Ball track: where the ball rolls
Rotor: the spinning part of the wheel where the numbers are
Pockets: where the ball comes to rest
Clocking: simply another word for 'take timings of'. ie if you 'clock' the rotor or ball, you are simply clicking buttons to take timings of revolutions.
What Happens During a Spin
When the ball is released, it gradually slows down, loses momentum and falls from the ball track. Sometimes the ball hits a metal deflector (diamond) and falls without much bounce. Sometimes it bounces everywhere. Sometimes there is still a fair bit of ball bounce. And while you can never predict exactly where the ball will fall, YOU DONT NEED TO. You need only to predict roughly where the ball will fall with enough accuracy to overcome the casino's slight edge against you (house edge). For some wheels, this is very easily done. For other wheels, it is much more difficult.
Here are some of the principles that are typically used to predict where the ball will land with professional roulette prediction techniques:
Dominant Diamonds
On most wheels, the ball will tend to hit a specific diamond more frequently than others. You can check this for yourself at your local casino by creating a chart like the one shown left. At the very least, you will find there are some diamonds that the ball almost never hits, or perhaps some areas where the ball almost never falls from the ball track. This is not random, and inevitably leads to more predictable spin results.
Now that we know WHERE the ball will fall at least an inordinate amount of times, what if we knew what number was under this area WHEN the ball fell? This is easy to determine, and I'll explain how later.
Consistent Ball Timings
You may think that when the ball is released, the timings of each revolution is random. The reality is especially the last few ball revolutions of the ball occur with much the same ball timings. The right chart shows the revolution timings for the last few revolutions of the ball on three different spins. You can see they are all very similar. The very bottom row shows the sum of all timings from these last seven ball revolutions. The greatest deviation in timings is no less than 300ms (0.3 seconds).
This means that if we knew when the ball timing (speed) was about 1350ms per revolution (about 1.3s per revolution), then we'd know the ball has about 12,500ms (12.5s) before it likely hits the dominant diamond and falls. Again of course this wont happen every time. It only needs to happen enough of the time.
Do you need to know the precise ball speed to know when there are 7 ball revolutions remaining? NO, you can virtually guess when there are roughly 7 revolutions remaining. Do you need to know exactly how many milliseconds are remaining? NO, because the ball revolution timings for the last few revolutions are much the same. This means finding which number will be under the diamond when the ball hits it is very easy to determine. This is a critical to understand.
Ball Scatter
Ball scatter is basically ball bounce. Sometimes the ball will miss all diamonds. Sometimes it hits a different diamond to usual. But a lot of the time, the ball will hit the dominant diamond, then bounce roughly 9 pockets along before coming to rest. There is a lot more to it in reality, but from a simplistic perspective, this is scatter.
If you check your local casino's wheels and compare where the ball first touches the rotor to its final restring place, you will see the ball bounce is usually still quite predictable over 15-30 or so spins. How we apply this knowledge is explained later.
Visual Ballistics
So far we know that on many wheels, the ball will mostly fall in the same region (dominant diamond), then mostly bounce 9 or so pockets. On many wheels we can actually skip the step where we consider how far the ball bounces after it hits the dominant diamond. This is because there is a more direct approach as explained below:
If you had a method to determine when the ball is about 1300ms (1.3s) per revolution, at that precise moment, you could look at the number under the reference diamond and write it down. Then wait for the ball to fall and come to rest. This will leave you with a first and second number like 'A,B'. For example say you got 0,21. This will tell you that the ball landed 5 pockets clockwise of your initial 'reference' number. See the left image for reference.
This tells us that starting from our REFERENCE NUMBER (A), the ball has about 12.5 seconds left before it hits the dominant diamond and bounces about 9 pockets, and ends up about +5 pockets from the reference number. Where the ball comes to rest is the WINNING NUMBER (B).
You may need to read this a few times, but the concept is very simple. Also see the video below which explains the concept too.

What I've explained above is a very simple method of beating roulette, or more like the science behind a method called 'visual ballistics'. The key component of any visual ballistics method is how you determine when the ball is at the targeted speed. Because when you have identified that target speed, you will know the ball has the same ball revolutions left before it falls and bounces however many pockets.
Can you virtually GUESS when the ball has 1 revolution remaining? How about 2 or 3 revolutions remaining? How about 5 or 6? It really is not at all difficult. If you can be accurate to within 1 ball revolution, then you can achieve exactly the same accuracy as most roulette computers without needing any device. Remember, you don't need to measure accuracy to within 5ms, 20ms or even 100ms because you are only determining how ball ball revolutions are remaining, and this automatically tells you the remaining ball travel time. You can be very sloppy and still be correct most of the time. And that's as accurate as you need to be to equal the accuracy as most roulette computers.
In a follow-up video I'll release soon, I'll teach you a method that can accurately tell you how many ball revolutions are remaining. And you will achieve the same accuracy as almost every roulette computer.
The Basic Roulette Computer Algorithm
This is what most roulette computer sellers don't want you to know. If you understand all of the above, you'd see how incredibly simple it all is. You'd also understand how you can afford to be very sloppy, and can just about guess how many revolutions are remaining and you'll still very accurately determine how many milliseconds are left before the ball falls. It is essential to note that ALL roulette computers use the above principles. You can look at the demonstration videos of basic roulette computers, and use basic visual ballistics to achieve almost exactly the same accuracy - without even using any electronic device. But because sellers want to make their products seem more competitive and exclusive, they'll tell you their devices are highly sophisticated with unparalleled accuracy.
Visual ballistics vs a Basic Roulette Computer
The main difference between typical visual ballistics and a basic roulette computer is that roulette computers are EASIER to use. There is no difference in accuracy between a skilled visual ballistic and computer player. Why? Because they both do exactly the same thing. They both just estimate when there are 7 or so ball revolutions remaining. They both 'tune' by looking at how far the actual winning number is from the reference number, then making a simple adjustment.
How Basic Roulette Computers Work
First the player finds a wheel where the ball mostly hits a particular diamond. Most wheels are like this. There are a few other basic procedures to evaluate a wheel, but this is just a simplified example. The player can create a small diagram l.ike the one shown left.
To use the computer, the player waits for the ball to be released then clicks a hidden button each time the ball passes a particular reference point (such as a diamond / metal deflector). This determines the timing of ball revolutions.
The player keeps clicking the hidden button until the time interval between clicks passes a certain threshold - this is when the ball is at a specific speed. When this threshold is passsed, the computer will vibrate at which time the player notes which number is under the reference diamond. Let's say it was number 32 (number A). This is an un-tuned prediction so we call it the RAW prediction. Then the player waits for the ball to fall and come to rest in a pocket. Let's say the winning number is 6 (number B). If we look at the distance between each number (A and B) in the chart left, we see this is +9 pockets (9 pockets clockwise) from the first to the second number.
It is important to understand that when the computer vibrates, this is telling the player that the ball has reached a target speed. And from this point, even on different spins, the ball will complete mostly the same number of revolutions before it likely hits the dominant diamond then falls.
The player repeat this process for 30-60 spins and add each jump value to a chart like the one shown left. After enough spins, we will find that certain areas of this chart have groupings of high bars (called 'peaks').
In the chart shown left, the peak is at about +10 pockets. This means for the player to win, they need to place bets around +10 pockets from the 'raw prediction' (Number 'A').
To Simplify
The player just keeps clicking a button until the interval between clicks is the say greater than 1,000ms (1 second). When this happens, the computer vibrates to inform the player the target ball speed is reached. From that point, the ball will mostly complete 5 or so revolutions before it hits the dominant diamond then bounces much the same distance.
Roulette Logarithm
To know where to bet each spin, the player notes the number under the reference diamond when the vibration is felt, then compares how far the ball actually lands from this original number. Then to know where to bet, the player just makes the adjustment on each spin.
Sounds simple enough? Almost every roulette computer you will find for sale will do only the very basics as explained above. It was all you needed 50 years ago, but beating modern wheels in modern casinos is far more complex.
Common Visual Ballistics Deception
Some sellers of visual ballistic methods will charge you thousands of dollars to learn visual ballistics methods you have learned here for free. Before you paid them, they would have told you that the method they teach is the best. But the truth is visual ballistic methods are all very similar. They all use exactly the same principles. Certainly some visual ballistic methods are overall better than others, but the differences are not often significant. One exception is if the method relies on a consistent rotor speed for accuracy to be achieved. For example, one individual claims his visual ballistics method is best because it enables you to obtain a visual ballistics prediction when the ball is at any speed. This may sound great, and he lures in uninformed people. But the reality is the method relies on the player having an unrealistic top-view of the wheel, god-like skill, and a rotor speed that is almost identical on all spins. The reality is such a methods cannot be applied in real casino conditions. Even slight variations in rotor speeds alone eliminate accuracy. On the other hand, one of his competitors who he unjustly attacks teaches a far better method that doesn't require consistent rotor speeds. So you need to be very careful about who you believe, or rather understand the principles for yourself, so you understand what is feasible.
NASA's roulette computer, or snake oil?
Roulette Logarithms In Exponential
Roulette computers that you can buy typically range from $500 - $5000, yet most do exactly the same thing. How is the price difference justified? IT ISN'T. Don't just take my word for it. So you know this for yourself, try using visual ballistics on their demonstration videos, and you'll achieve the same accuracy without even using a roulette computer. Remember that no matter what a vendor tells you, you can easily expose nonsense with careful testing and research of your own. If you prefer to just take other people's word for it, don't expect to know the truth.
Of course every merchant is expected to promote their product, and it is common for merchants to stretch the truth about their products. However, the gambling industry has far more deception and false advertising in it than any other area of business I've ever known. It seems every roulette computer seller wants you to believe their device is space-age technology that cannot be obtained anywhere else. But the reality is almost every roulette computer uses the same basic algorithm explained on this page, and the accuracy differences between them are virtually negligible. Don't let technical talk and fancy charts fool you. When you break it all down, you are left with a salesman trying to sell a basic computer that is no better than visual ballistics.
Karl Roulette Logarithm
The simplest roulette computer I offer is called the 'Basic roulette computer'. No fancy names. It is just a basic roulette computer using the basic design described above. It is FREE to my roulette system players because it realistically can beat only perhaps 5% of wheels, and still the accuracy is nowhere what could be achieved. Other device sellers sell comparable devices with exactly the same accuracy for between $500 - $5,000. Again, the price differences are not justified. I distribute this device for FREE. You can achieve exactly the same accuracy with basic visual ballistics methods. Alternatively you could buy a device for $2000 that does exactly the same thing, except the vendor blatantly lies and claims it does much more, and is the most accurate device available anywhere.
Roulette Logarithm Strategy
The various roulette computers I offer are compared to devices from other vendors at the roulette computer comparison page. There you can better understand the difference between a simplistic device that can only beat easily beaten wheels, and a device that squeezes every last bit of predictability from a roulette wheel while making application practical, covert and easy.